Quantum computers require controlled encoding to protect computations from environmental noise. Two experiments have achieved such encoding using what are known as infinite-dimensional quantum systems.
Transmitting or manipulating information in a noisy environment typically requires some form of encoding and error correction. If these precautions are necessary when information is carried by classical physical systems, they are even more so when the carriers are fragile quantum systems. However, quantum encoding is notoriously difficult, because the laws of quantum mechanics impose severe constraints — for example, a single quantum object cannot be copied, which hinders simple encoding schemes. Consequently, the manipulation of encoded quantum systems, which is necessary for error correction, can be extremely involved. In two papers in Nature, Flühmann et al.1 and Gao et al.2 report promising methods for encoding and manipulating quantum information using, respectively, the state of motion of a trapped ion and the state of multiple photons in superconducting cavities.
Quantum systems can be classified into two categories, depending on the dimensionality of the parameter space that is needed to describe their features accurately. On the one hand, there are quantum features that require a finite dimension. An example is the magnetic moment of an electron, which has only two distinguishable states and is therefore represented in a 2D space. Such features are called discrete variables, and they are intrinsically digital3. On the other hand, there are quantum features that have infinitely many distinguishable states, such as the position of a quantum harmonic oscillator — the quantum-mechanical version of a mass suspended on a spring. These features are known as continuous variables and are intrinsically analog4.
From the transmission of data over the Internet to data analysis, classical information is typically encoded in digital form because of the existence of robust digital error-correction schemes. Therefore, when it comes to quantum information, it is natural to consider discrete-variable systems, such as two-state systems called quantum bits (qubits). This approach has been well explored in the past few decades. However, error correction remains challenging, and it ultimately requires a single logical qubit (a qubit that can be used for programming) to be suitably encoded into many physical qubits (actual implementations of qubits). In other words, it is necessary to enlarge the dimension of the space, and the choice of discrete-variable systems then turns out to be not so obvious.
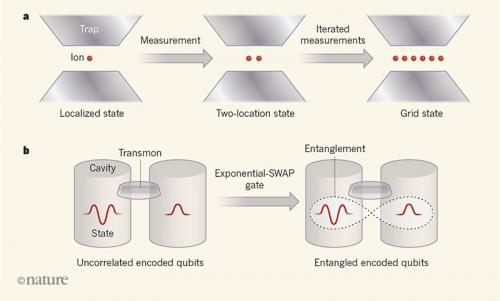
Consequently, various methods have been proposed for encoding a logical qubit into the infinite-dimensional space offered by a single continuous-variable system, rather than by many discrete-variable ones. A celebrated continuous-variable encoding is the Gottesman–Kitaev–Preskill (GKP) scheme5, which was proposed in 2001. A crucial feature of this scheme is that most encoded operations (manipulations of logical qubits) belong to a set of operations that, in general, can be easily implemented6. However, a method for generating GKP-encoded qubits has been elusive. Flühmann and colleagues have succeeded in this endeavour by preparing a quantum harmonic oscillator in a state that resembles a GKP-encoded qubit. They used an architecture consisting of an oscillator in the form of an atomic ion that is free to oscillate along one axis of an electromagnetic trap.
The authors’ technique involves two steps (Fig. 1a). First, the ion is confined in a state of motion that has a well-defined position in the trap, using a technique that exploits energy loss to reduce the uncertainty in the ion’s motion7. Second, a sequence of measurements is taken using laser pulses, after which the ion is delocalized in specific regions of the trap, akin to a grid. Flühmann et al. managed to prove that these grid states are a good approximation of a GKP-encoded qubit. Importantly, they found that such encoded states could be manipulated at will, achieving fidelities (a measure of the similarity of quantum states) of 87–97%.
As mentioned, GKP encoding is not the only option, and other schemes exist that can be more convenient, depending on the system at hand. It is therefore desirable to be able to manipulate logical qubits using operations that are independent of the encoding. An example of such an operation is the exponential-SWAP gate8 (the exponential function of the operation that swaps two logical qubits), which was proposed in 2016. A crucial feature of the exponential-SWAP gate is that any algorithm can be run by repeated use of the operation, interspaced with other operations that act on single logical qubits only. Gao and colleagues realized the exponential-SWAP gate in an architecture composed of superconducting cavities that contain microwave fields and that are coupled and measured using superconducting electrical components called transmons.
In the authors’ experiment, logical qubits are encoded in the states of multiple photons in two cavities — another infinite-dimensional system (Fig. 1b). Gao et al. realized two different encodings: Fock encoding, which is based on the number of photons; and coherent-state encoding, which uses the superposition (summation) of particular quantum states called coherent states. Notably, the latter encoding was previously shown to extend the lifetime of a logical qubit beyond what is achievable using any of its physical constituents alone9. On the basis of the experimental techniques that were developed to extend the lifetime, Gao and colleagues demonstrated the exponential-SWAP gate by implementing a controlled exchange of photons between the two cavities. Crucially, this operation is deterministic, and works with both Fock encoding and coherent-state encoding, reaching fidelities of 85% and 60%, respectively.
These two experiments demonstrate two cornerstones of quantum computation using continuous variables: GKP-encoded qubits and the exponential-SWAP gate. Even if the current set-ups do not yet reach the quality required for a fully fledged error-correction scheme, they represent a major step towards this objective. In particular, improvements are required to increase the lifetime of the encoded qubits and to allow the possibility of concatenating many levels of error correction. A common trait of the experiments is that they use ancillary discrete-variable systems to manipulate the continuous variables. Hybrid continuous and discrete schemes can therefore, in principle, be devised to improve the performance of both experiments10.
Besides full error correction and large-scale computation, which are probably still some distance away, the techniques developed in these studies could have other applications. For example, GKP-encoded qubits can be used for high-resolution displacement sensing11, whereas exponential-SWAP gates integrated in a circuit might enable the demonstration of specific instances in which quantum computation outperforms its classical counterpart12. More generally, the exquisite level of control attained in these two very different architectures shows that infinite-dimensional systems, despite their analog character, are a cutting-edge contender in the race for advanced quantum information processing. Scientists now have a remarkable source of inspiration to see what could be achieved using other emerging continuous-variable architectures, such as optomechanical and electromechanical systems and integrated optics.